CBSE Class 6th, 7th, 8th, 9th, & 10th | Help Guide | Solved Exercises | MCQs | Questions & Answers | Sample Papers
Sunday 18 November 2012
Saturday 27 October 2012
At age10 Shravan and at 12 Sanjay Kumaran are Co-Founders of GoDimensions
We develop Application for new World to make life easier. Our Focus is to develop Mobile Application. Primarily in the area of Education, Games, Lifestyle & Convenience.
This is what their's website homepage says.....
Shravan is 12 year old studying 8th Grade and Sanjay is 10 year old studying 6th Grade
They are both Co-Founders of GoDimensions (http://www.godimensions.com)
Shravan (10) and Sanjay Kumaran (12), two brothers from Chennai have created mobile phone applications that have witnessed over 10,000 downloads across the world already.
Sindhuja Rajaraman: Meet the 14-year CEO of Seppan Entertainment
With an IQ of 225, K. Vishalini from Palayamkottai is the Best !!!
- She has a tested IQ of 225, much higher than the current World record holder(210)
- She has passed Microsoft Certified Professional and Cisco Certified Network Associate (CCNA) with more than 90% when she was just 10 years old - a world record again.
- She regularly now gets invited for "guest lectures" on Engineering topics at International conferences and by prestigious institutions.
Kirtana Vallabhaneni UK Young Scientist of the Year 2012
Deepika Kurup a Malayali girl is America’s Top Young Scientist
Wednesday 24 October 2012
India superpower ! (?) Says Ron Marz, and Rovolt’s CEO Manish Sinha
As discovered by NewsHut and as told to :Sumedha Deo, HT
Most of us have memories of sneakily reading comics hidden in our textbooks and prancing around the house with a dupatta-cape around our necks. Comic book writer Ron Marz has played a part in this childhood dream of becoming a superhero fulfilled — he’s worked on characters like the Green Lantern and Silver Surfer.
See Promo Video
Most of us have memories of sneakily reading comics hidden in our textbooks and prancing around the house with a dupatta-cape around our necks. Comic book writer Ron Marz has played a part in this childhood dream of becoming a superhero fulfilled — he’s worked on characters like the Green Lantern and Silver Surfer.
Saturday 30 June 2012
CBSE Class 7th (VII) History- Our Pasts - II :Chapter 3. The Delhi Sultanate-Solved Exercises
Intext Question
Page No.32Question1. Do you think the circle of justice is an appropriate term to describe the relationship between the king and his subjects?
Answer. Yes, I think, the circle of justice is an appropriate term to describe the relationship between the king and his subjects
Intext Question Page No.33
Question 1. Express Minhaj's ideas in your own words. Do you think the Raziyya shared these ideas? Why do you think it was so difficult for a woman to be a ruler?
Answer:
1. According to Minhaj, God has created a social order in which women is subordinate to man. Therefore, a women like Raziyya doesnot have right to rule. It is totsaly against the ideal social order created by God.
2. I think Raziyya did not share these ideas.
3. It was very difficult for a women to be a ruler because of her belonging to a subordinate gender, according to the social set up at that time.
Intext Question Page No.35
Question 1. But how complete and effective was its control over such a vast territory?
Answer. The Sultanate did not have complete and much effective control over such a vast territory, except under the rule of Alluddin Khalji.
Intext Question Page No.37
Question 1. Compare figures 2,3 ,4 and 5. What similarities ans differences do you notice amongst the the mosques?
Answer:
Similarities:
1. Every mosque has a big entrance door.
2. Every mosque's entrance door is extended to both sides in the corridor.
Differences:
1. The designs around the entrance door become complex and intricate from fig.2 to fig.5.
2. The small window over the entrance door can be seen only in three mosques in Fig. 3, 4, 5. But Fig. 3 Shows three such windows. Whereas Figs. 4 and 5 shows only single window over the entrance.
3. There is a boundary around the dome over the entrance door in Fig.5. This is not seen in any other figure.
Wednesday 9 May 2012
CBSE Class 6th ( VI) Mathematics Chapter 8. Decimals: Exercise 8.6 Solved
Things to remember...
- To understand the parts of one whole (i.e. a unit) we represent a unit by a block. One block divided into 10 equal parts means each part is 1/10 (one-tenth) of a unit. It can be written as 0.1 in decimal notation. The dot represents the decimal point and it comes between the units place and the tenths place.
CBSE Class 6th ( VI) Mathematics Chapter 8. Decimals: Exercise 8.4
1. Express as rupees using decimals.
- 5 paise
- 75 paise
- 20 paise
- 50 rupees 90 paise
- 725 paise
CBSE Class 6th ( VI) Mathematics Chapter 8. Decimals: Exercise 8.5
Things to remember
- To understand the parts of one whole (i.e. a unit) we represent a unit by a block. One block divided into 10 equal parts means each part is 1/10(one-tenth) of a unit. It can be written as 0.1 in decimal notation. The dot represents the decimal point and it comes between the units place and the tenths place.
CBSE Class 6th ( VI) Mathematics Chapter 8. Decimals: Exercise 8.3
1. Which is greater?
- 0.3 or 0.4
- 0.07 or 0.02
- 3 or 0.8
- 0.5 or 0.05
- 1.23 or 1.2
- 0.099 or 0.19
Saturday 5 May 2012
CBSE Class 6th ( VI) Mathematics Chapter 3. Playing with Numbers: Exercise 3.7 Solved
1. Renu purchases two bags of fertiliser of weights 75 kg and 69 kg. Find the maximum
value of weight which can measure the weight of the fertiliser exact number of times.
Answer:
Answer:
| The Highest Common Factor (HCF) of 75kg and 69kg by weight will be the maximum
value of weight which can measure the weight of the fertiliser exact number of times. To find HCF first we have to find prime factorisation of given numbers by weight i.e. 75 and 69 |
Monday 16 April 2012
CBSE Class 6th ( VI) Mathematics Chapter 8. Decimals: Exercise 8.2
Sunday 15 April 2012
CBSE Class 6th ( VI) Mathematics Chapter 8. Decimals: Exercise 8.1 Solved
CBSE Class 6th ( VI) Mathematics Chapter 7. Fractions: Exercise 7.6
Things to remember.....
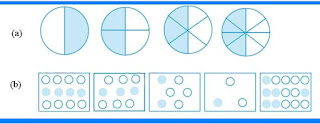
- A fraction is a number representing a part of a whole. The whole may be a single object or a group of objects.
- When expressing a situation of counting parts to write a fraction, it must be ensured that all parts are equal.
- In 5/7 , 5 is called the numerator and 7 is called the denominator.
- Fractions can be shown on a number line. Every fraction has a point associated with it on the number line.
Thursday 12 April 2012
CBSE Class 6th ( VI) Mathematics Chapter 7. Fractions: Exercise 7.5 Solved
Thursday 5 April 2012
CBSE Class 6th ( VI) Mathematics Chapter 7. Fractions: Exercise 7.4
Let us Remember..
- Fractions with same denominators are called like fractions. For example, 1/15, 2/15, 3/15, 8/15 are all like fractions.
- Fractions with different denominators are called unlike fractions. 11/27 and 9/28 are unlike fractions
- For given any two fraction the fraction with the same denominator, the fraction with the greater numerator is greater. For example Between 4/5 and 3/5, 4/5 is greater. Between 11/20 and 13/20, 13/20 is greater and so on.
Tuesday 3 April 2012
CBSE Class 6th ( VI) Mathematics Chapter 6. Integers: Exercise 6.3
Remember
- Every positive integer is larger than every negative integer.
- Zero is less than every positive integer.
- Zero is larger than every negative integer.
- Zero is neither a negative integer nor a positive integer.
- Farther a number from zero on the right, larger is its value.
Monday 2 April 2012
CBSE Class 6th ( VI) Mathematics Chapter 6. Integers: Exercise 6.2
Remember
- Every positive integer is larger than every negative integer.
- Zero is less than every positive integer.
- Zero is larger than every negative integer.
- Zero is neither a negative integer nor a positive integer.
- Farther a number from zero on the right, larger is its value.
CBSE Class 6th ( VI) Mathematics Chapter 6. Integers: Exercise 6.1
Remember
- Every positive integer is larger than every negative integer.
- Zero is less than every positive integer.
- Zero is larger than every negative integer.
- Zero is neither a negative integer nor a positive integer.
- Farther a number from zero on the right, larger is its value.
Thursday 29 March 2012
CBSE Class 6th ( VI) Mathematics Chapter 7. Fractions: Exercise 7.3 Solutions
CBSE Class 6th ( VI) Mathematics Chapter 7. Fractions: Exercise 7.2 Solutions
- Proper Fraction :
- A proper fraction is a number representing part of a whole.
- In a proper fraction the denominator shows the number of parts into which the whole is divided and the numerator shows the
number of parts we have taken out. - In a proper fraction the numeratoris always less than the denominator.
CBSE Class 6th ( VI) Mathematics Chapter 7. Fractions: Exercise 7.1 Solutions
Remember....
- A fraction means a part of a group or of a region.
5
is a fraction. We read it as "five-twelfths". 12 - Here "12" stand for the number of equal parts into which the whole has been divided.
- And "5" stand for the number of equal parts which have been taken out.
- Here 5 is called the numerator and 12 is called the denominator.
Wednesday 21 March 2012
CBSE Class 6th ( VI) Mathematics Chapter 3. Playing with Numbers: Exercise 3.6
Remember...
- The Highest Common Factor (HCF) of two or more given numbers is the highest (or
greatest) of their common factors. It is also known as Greatest Common Divisor (GCD).
(a) 18, 48 (b) 30, 42 (c) 18, 60 (d) 27, 63
(e) 36, 84 (f) 34, 102 (g) 70, 105, 175
(h) 91, 112, 49 (i) 18, 54, 81 (j) 12, 45, 75
Wednesday 14 March 2012
CBSE Class 6th ( VI) Mathematics Chapter 3. Playing with Numbers: Exercise 3.5
Remember...
- if a number is divisible by another number then it is divisible by each of the factors of that number.
- If a number is divisible by two co-prime numbers then it is divisible by their product also.
- If two given numbers are divisible by a number, then their sum is also divisible by that number.
- If two given numbers are divisible by a number, then their difference is also divisible by that number.
Tuesday 13 March 2012
CBSE Class 6th ( VI) Mathematics Chapter 3. Playing with Numbers :Exercise 3.4
1. Find the common factors of :
(a) 20 and 28 (b) 15 and 25 (c) 35 and 50 (d) 56 and 120
Answer:
| (a) 20 and 28 | |
| Factors of 20 are: | 1, 2, 4, 5, 10, 20 |
| Factors of 28 are: | 1, 2, 4, 7, 14, 28 |
| Common factors of 20 and 28 are 1, 2, 4 | |
Saturday 10 March 2012
CBSE Class 6th ( VI) Mathematics Chapter 3. Playing with Numbers :Exercise 3.3
1. Using divisibility tests, determine which of the following numbers are divisible by 2;
by 3; by 4; by 5; by 6; by 8; by 9; by 10 ; by 11 (say, yes or no):
by 3; by 4; by 5; by 6; by 8; by 9; by 10 ; by 11 (say, yes or no):
| Number | Divisible by | ||||||||
| 2 | 3 | 4 | 5 | 6 | 8 | 9 | 10 | 11 | |
| 128 | Yes | No | Yes | No | No | Yes | No | No | No |
| 990 | .... | .... | .... | .... | .... | .... | .... | .... | .... |
| 1586 | .... | .... | .... | .... | .... | .... | .... | .... | .... |
| 275 | .... | .... | .... | .... | .... | .... | .... | .... | .... |
| 6686 | .... | .... | .... | .... | .... | .... | .... | .... | .... |
| 639210 | .... | .... | .... | .... | .... | .... | .... | .... | .... |
| 429714 | .... | .... | .... | .... | .... | .... | .... | .... | .... |
| 2856 | .... | .... | .... | .... | .... | .... | .... | .... | .... |
| 3060 | .... | .... | .... | .... | .... | .... | .... | .... | .... |
| 406839 | .... | .... | .... | .... | .... | .... | .... | .... | .... |
Friday 9 March 2012
CBSE Class 6th ( VI) Mathematics Chapter 3. Playing with Numbers :Exercise 3.2
1. What is the sum of any two (a) Odd numbers? (b) Even numbers?
Answer:
(a) The sum of any two Odd numbers is an Even number. i.e. 1+3=4, 3+5=8, 5+7=12
(a) The sum of any two even numbers is an Even number. i.e. 2+4=6, 4+6=10, 12+8=20
2. State whether the following statements are True or False:
Answer:
(a) The sum of any two Odd numbers is an Even number. i.e. 1+3=4, 3+5=8, 5+7=12
(a) The sum of any two even numbers is an Even number. i.e. 2+4=6, 4+6=10, 12+8=20
2. State whether the following statements are True or False:
Wednesday 7 March 2012
CBSE Class 6th ( VI) Mathematics Chapter 3. Playing with Numbers :Exercise 3.1
1. Write all the factors of the following numbers :
Answer:
| (a) 24 | (b) 15 | (c) 21 |
| (d) 27 | (e) 12 | (f) 20 |
| (g) 18 | (h) 23 | (i) 36 |
| (a) 24 |
|
Monday 5 March 2012
CBSE Class VI ( 6th) Mathematics Chapter 2. Whole Numbers : Exercise 2.3
Question 1. Which of the following will not represent zero:
Answer:
| (a) | a + 0 |
| (b) | 0 × 0 |
| (c) | 0 |
| 2 |
| (d) | 10×10 |
| 2 |
Answer:
| (a) | a + 0 | and | (d) | 10×10 |
| 2 |
Sunday 4 March 2012
CBSE Class 7th (VII) English | Chapter 9. A Bicycle in Good Repair-Solved Exercises
Intext Questions (Comprehension Check (Page 128))
- Question . "I got up early, for me" It implies that
- he was an early riser
- he was a later riser.
- he got up late that morning.
Mark the correct answer
CBSE Class 6th ( VI) Mathematics Chapter 2. Whole Numbers : Exercise 2.2
Question 1. Find the sum by suitable rearrangement:
(a) 837 + 208 + 363 (b) 1962 + 453 + 1538 + 647
Answer:
(a) 837+208+363
= (837+363)+208
= 1200+208
= 1408
(a) 837 + 208 + 363 (b) 1962 + 453 + 1538 + 647
Answer:
(a) 837+208+363
= (837+363)+208
= 1200+208
= 1408
Saturday 3 March 2012
CBSE Class 7th (VII) English | Chapter 8. Fire: Friend and Foe-Solved Exercises
Intext Questions (Comprehension Check (Page 118))
Question 1.Mark the correct answer in each of the following.- Early man was frightened of
- lightning and volcanoes.
- the damage caused by them.
- fire.
Friday 2 March 2012
CBSE Class 7th (VII) English | Chapter 7. The Invention of Vita-Wonk - Solved Exercises
Word Meaning | ||
| Word | Meaning in English | Meaning in Hindi |
| Whiskers | moustache | मूंछ |
| Grimalkin | old cat | वृद्ध बिल्ली |
| Cattaloo | a crossbreed between a cow and a buffalo. | एक गाय और भैंस के बीच एक संकर प्रजाति |
| Knuckle bone | bone of knuckles | अंगुली की हड्डी |
| Stinging slug | bad smelling mollusc | चुभने काउंटर |
| Venomous | poisonous | विषैला |
| Shriveling | wrinkle | झुर्री |
CBSE Class 7th (VII) English | Chapter 6. Expert Detectives - Solved Exercises
Word Meaning | ||
| Word | Meaning in English | Meaning in Hindi |
| Monster | Horrible figure | राक्षस, विकराल दैत्य |
| Stash | place of hiding | छिपाने की जगह |
| Starve | without food | भूखा |
| Scars | marks of cut or injury or burn | निशान |
| Annoyed | angry | नाराज, अप्रसन्न |
| Stubborn | one who doesn't listen or obey anyone | जिद्दी |
| Accomplice | to assist or one who assist in doing a crime | सहकारी, सह - अपराधी |
CBSE Class 7th (VII) English - Chapter 5. Quality - Solved Exercises
Textbook Questions (Working with the Text)
Answer the following questions.Question 1. What was the author's opinion about Mr. Gessler as a bootmaker?
Answer: According to the author, Mr. Gessler was the best shoemaker in the city. He was a perfect artist who had the same skill, pride and respect fo his trade as any other artist had.
Question 2. Why did the author visit the shop so infrequently?
Answer: The shoe made by Mr. Gessler used to last terribly longer than the usual, therefore, he visited the shop so infrequently.
Wednesday 29 February 2012
CBSE Class 7th (VII) English -Chapter 4. The Ashes That Made Trees Bloom - Solved Exercises
Intext Questions ( Comprehension Check Page,60)
Question 1. Why did the neighbor kill the dog?Answer. The neighbours on hearing the good luck bought to couple by the dog, coaxed the dog and took it to the field. The dof scratched and powed the ground under a pine tree. When digging the ground the neighbor didn't get gold, in anger killed the dog and flung him into the hole.
CBSE Class 7th (VII) English Chapter 3. Gopal and the Hilsa Fish Solved Exercises
Textbook Question (Working with the text)
Answer the following questions.Question 1. Why did the king want no more talk about the hilsa-fish?
Answer: The king did not want more talks about the hilsa-fish because he had become fed up of talks. Everyone in the court, in the market as well as all people of the city talking about hilsa-fish.
Question 2. What did the king ask Gopal to do to prove that he was clever?
Answer: The king asked Gopal to buy hilsa-fish and bring it to the court without letting anybody talk a single word about the hilsa-fish throughout the way.
CBSE Class 7th (VII) English Chapter 2. A Gift of Chappals - Solved Exercises
Comprehension Check (Page,22)
Page No.17Question 1. What is the secret that Meena shares with Mridu in the backyard?
Answer. Meena tols Mridu about the small kitten which was lying inside a torn football lined with sacking and filled with sand, lapping milk from a coconut half-shell. She told Mridu that they found outside the gate that morning and that a secret which their mother didn't know
Question 2. How does Ravi get milk for the kitten?
Answer: Ravi told his mother hungry and wanted to drink milk. The mother gave him and asked him to keep the tumbler back. Ravi told her that he would wash it himself after finishing the milk. And this was how he got the milk for kitten.
Tuesday 28 February 2012
CBSE Class VII (7th) English Lesson 1 : Three Questions - Solved Exercises
Part (1)
Question 1. Why did the king want to know answer to three questions?
Answer. The king wanted to know answer to three questions because, he thought that if he new the answers then he would never fail.
Question 2. Messengers were sent throughout the kingdom.
1. to fetch wise men.
2. to find answers to the question.
3. to look for wise hermit.
4. to announce a reward for those who could answer to the question.
Question 1. Why did the king want to know answer to three questions?
Answer. The king wanted to know answer to three questions because, he thought that if he new the answers then he would never fail.
Question 2. Messengers were sent throughout the kingdom.
1. to fetch wise men.
2. to find answers to the question.
3. to look for wise hermit.
4. to announce a reward for those who could answer to the question.
Sunday 15 January 2012
CBSE Class 10th Science | Chapter 4. Carbon and its Compounds | Solved Exercises
Points to Remember - What you have learnt
- Carbon is a versatile element that forms the basis for all living organisms and many
of the things we use. - This large variety of compounds is formed by carbon because of its tetravalency
and the property of catenation that it exhibits.
- Covalent bonds are formed by the sharing of electrons between two atoms so that
both can achieve a completely filled outermost shell.
Subscribe to:
Posts (Atom)


-Mathematics-Chapter-8-Decimals-Exesise-8-2-Q1.JPG)
-Mathematics-Chapter-8-Decimals-Exesise-8-1-Q1.JPG)